Exploration & Old

[Computational Media] Grass Hunt

Stream
January 30, 2015

A cool way to learn algorithms!

A hunting game that visualizes results of different methods of walking.

ScreenShots:1

  • Rest and result:

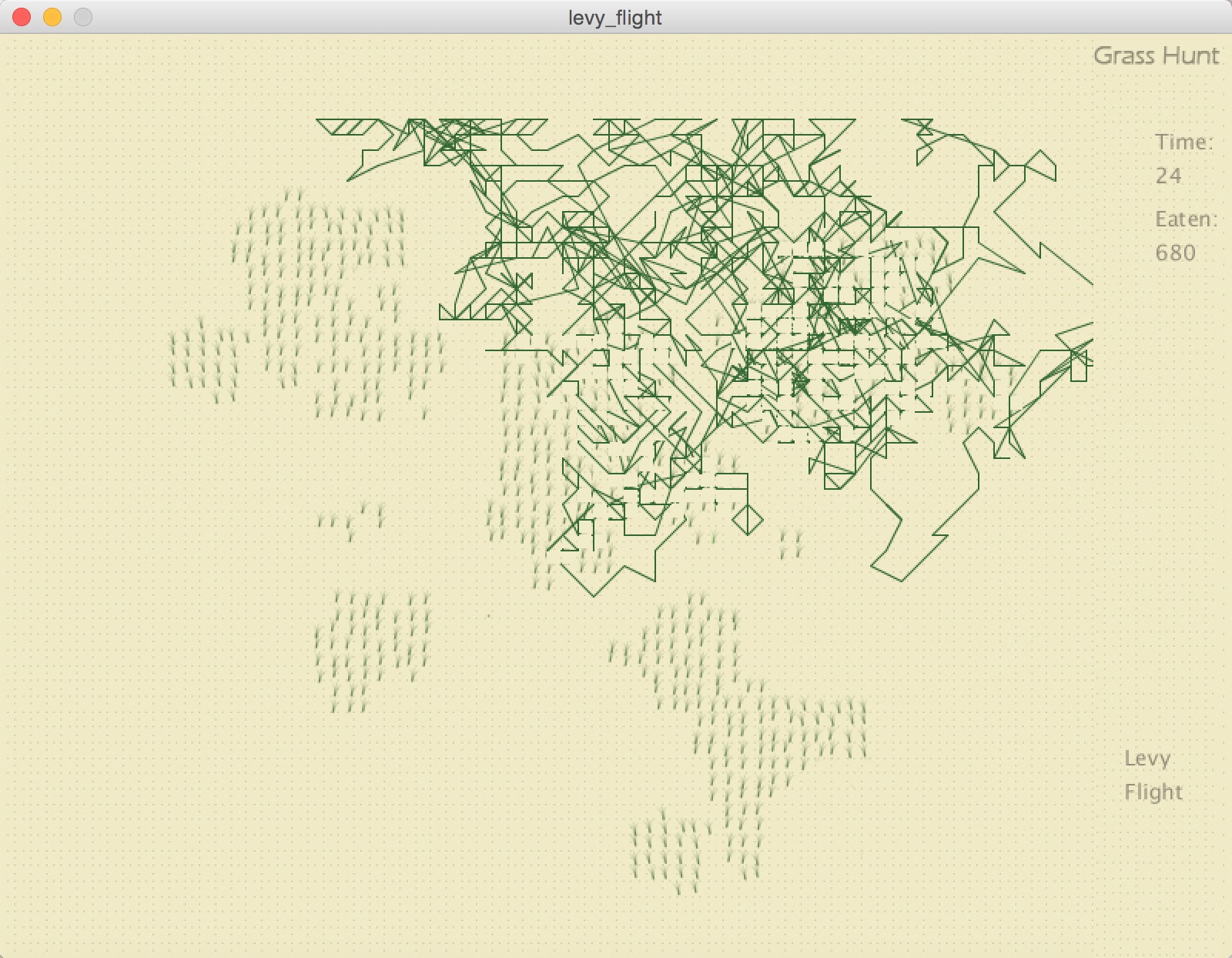
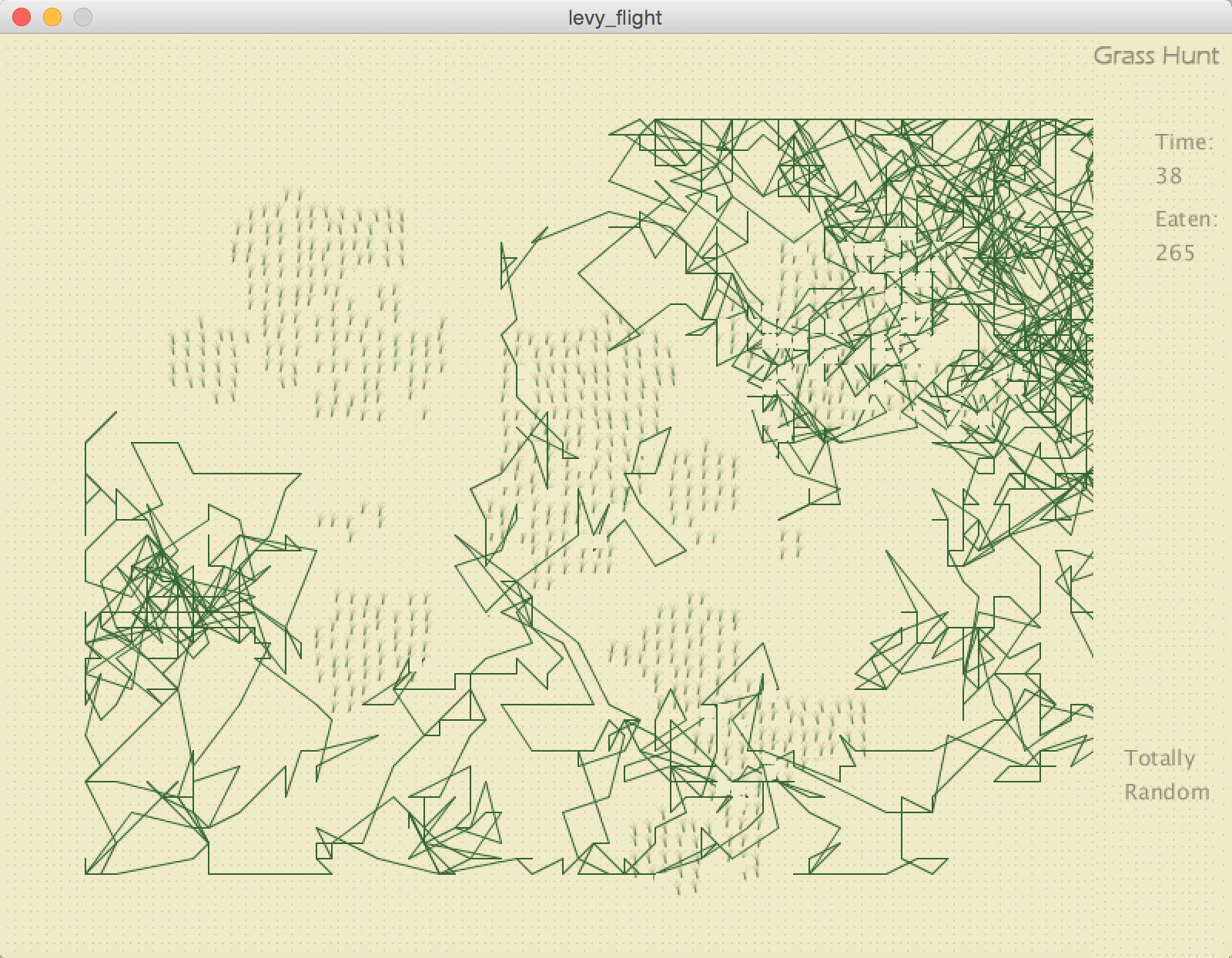
I made a comparison between the route of Levy Flight walk and the totally random walk. Here to see the route of different walk types. We can see the route of totally random is super messy while Levy Flight is much more organized.

2random

The average eaten number for both of the 2 types :

I calculated the number 5 times for each of them. The average eaten number for Levy Flight is 407, while the totally random is 233.

So. Be smart to choose a better way of walking!
Github codes: